THC Publishing

Contact

1. Neural Network Structure

A neuron does nothing unless the collective influence of all inputs reaches a threshold level. A nonzero-threshold neuron is computationally equivalent to a zero-threshold neuron with an extra link connected to an input that is always held at -1.

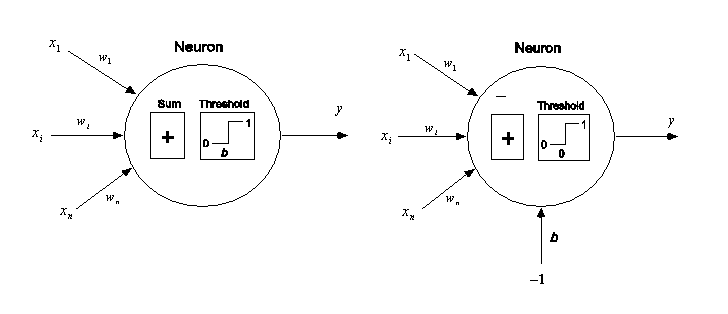
We have

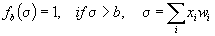
or equivalently

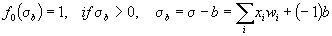
Therefore, a neural network uses zero-threshold neurons with augmented input with -1.

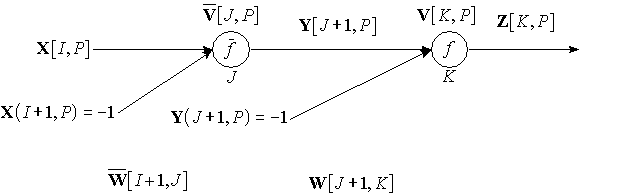
where

(Eq 1)

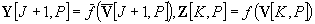
(Eq 2)

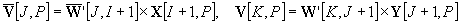
We have an error between the actual output Z and the desired output D

(Eq 3)

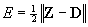
we will find the weights W and

to eliminate the error. We have

(Eq 4)

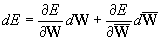
if

(Eq 5)

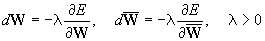
then

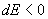
since E > 0, E will reduce to zero.

2. Calculation of Error Gradient

In terms of components, by Eq.(1), (2) and (3), we have

(Eq 6)

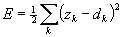
(Eq 7)

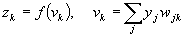
(Eq 8)

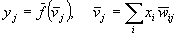
By Eqs.(6) to (8) and from the chain rule, we have for a certain output node k

(Eq 9)

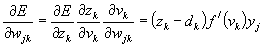
and for a certain hidden node j

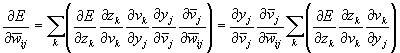
or

(Eq 10)

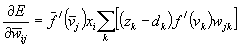
where

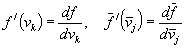
So

(Eq 11)

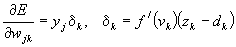
(Eq 12)

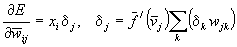
3. Activating Functions

A step function is replaced by a differentiable sigmoid function. Typical activating functions are

• Logistic function
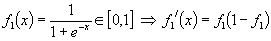
• Bipolar logistic function
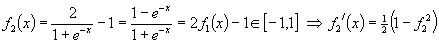
• Hyperbolic Tangent function

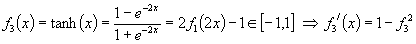
4. Conclusion

The weights W and 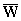are arbitrarily initialized and updated by the following sequence

• forward to compute the actual output
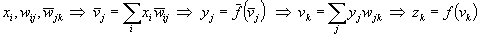
• Back Propagation==backward to compute the error gradient

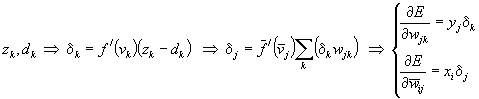
Then the weights are updated as follows

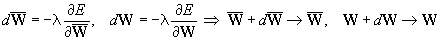
where l is a positive learning rate.

To calculate the error gradient, we have to start from the output to update the weight W and then go backward