GPS Principles: A Practical and Precise Approach
Mary Nguyen, Duy-Ky Nguyen, PhD
1. Introduction
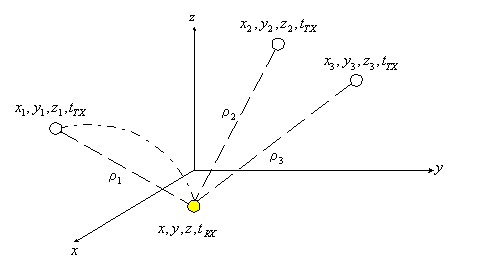
This section is about how to use satellite data to compute receiver potion and time. Assume we know positions of 3 satellites and transmit time tTX (or SV`s, space vehicles) and unknown receiver position and known receive time tRX , so we have 3 unknowns x, y, and z. We know from elementary algebra that we need 3 equations to solve these 3 unknowns
(Eq.1)
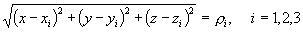
where
(Eq.2)
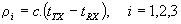
with constant c is speed of light (300,000 km/s)
To be valid, (Eq.1) requires a straight line (line of sight) between SV and receiver. However, (Eq.2) gives a curve which is exaggerated in the figure above as signal transmitted in a curve due to, say, refraction through media with different index like light. That`s why ri is called pseudo-range or pseudo-distance as range or distance implies straight line.
To count for incorrect time at user position, (Eq.1) is modified to be
(Eq.3)
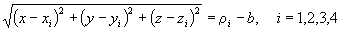
where additional equation is for unkown b as user clock bias error expressed in distance
(Eq.4)
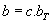
Therefore, to solve for user position and time, we need to solve the simultaneous equations below
(Eq.5)
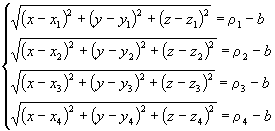
These equations are transcendental, so cannot be solved algebraically. They must be solved numerically and the more equations involved, the quicker in getting to the solution, so we need at least 4 SV`s for solution. If they were solved algebraically, we need only 4 equations, ie 4 SV`s.
The SV data, like position and time, are carried in SV message called ephemeris (ephemeredes in plural). The following sections are about SV data and several methods to solve (Eq.5) from basic to advanced, like using Kalman filter.
2. Navigation Data
GPS satellite sends navigation data in frames to GPS receiver to in solving (Eq.5). These data are in spherical coordinates and required to transformed into Cartesian ones required in (Eq.5).2.1. Signal Structure
GPS receivers get navigation data from satellite in frames with structures below.
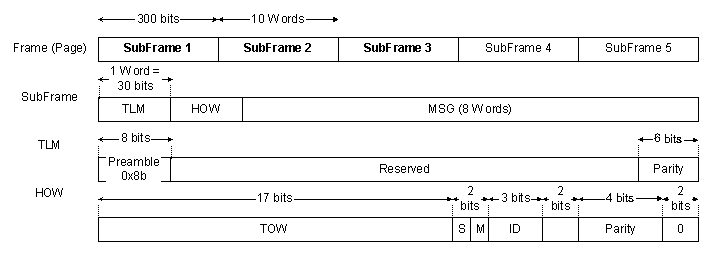
Every subframe has 10 words, 30 bits each, so 300 bits long. Each frame has 1st word for TLM (telemetry) with subframe boundary identifier (0x8b) and 2nd for HOW (Hand-Over Word) with time of week (TOW) in unit of 6 seconds where 0 is at mid-night Saturday and Sunday. For 1 week, we have 7*24*3600 = 604,800 seconds; so maximum TOW is 604,800/6 = 100,800; 100,799 actually.
Frame 1
| Description | Location | Numberof Bits | ScaleFactor | Unit | |
| Week Number | 61~70 | 10 | 1 | week |
Frame 2
| Description | Location | Numberof Bits | ScaleFactor | Unit | |
| Crs | Amplitude of the sine harmonic correction terms to the orbit radius | 69~84 | 16 | 2-5 | meter |
| Dn | Mean motion difference from computed value | 91~106 | 16 | 2-43 | Semicircle/sec |
| M0 | Mean anomaly at reference time | 107~114 121~144 | 16 | 2-31 | radian |
| Cuc | Amplitude of the cosine harmonic correction terms to the argument of latitude | 151~166 | 16 | 2-29 | |
| e | Eccentricity | 167~174 181~204 | 2-33 | ||
| Cus | Amplitude of the sine harmonic correction terms to the argument of latitude | 211~226 | 16 | 2-29 | radian |
 |
Square root of the semi-major axis | 227~234 241~264 | 32 | 2-19 | Meter1/2 |
| toe | Ephemeris reference time (seconds in the GPS week) | 277~286 | 16 | 24 | second |
Frame 3
| Description | Location | Numberof Bits | ScaleFactor | Unit | |
| Cic | Amplitude of the cosine harmonic correction terms to the angle of inclination | 61~76 | 16 | 2-29 | radians |
| W0 | Right Ascension at reference time | 77~84 91~114 | 32 | 2-31 | Semicircle |
| Cis | Amplitude of the sine harmonic correction terms to the angle of inclination | 121~136 | 16 | 2-29 | radians |
| i0 | Inclination angle at reference time | 137~144 151~174 | 32 | 2-31 | Semicircle |
| Crc | Amplitude of the cosine harmonic correction terms to the orbit radius | 181~196 | 16 | 2-5 | meter |
| w | Argument of Perigee | 197~204 211~234 | 32 | 231 | Semicircle |
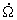 |
Rate of change of Right Ascension angle | 241~264 | 24 | 2-43 | Semicircle/sec |
| IDOT | Rate of change of inclination angle | 279~292 | 14 | 2-43 | Semicircle/sec |
2.2. Ephemeris Processing
GPS navigation Ephemeris data from satellite are converted to Cartesian coordinates required in (Eq.5).
WGS 84 value of the earth`s universal gravitational parameter
(Eq.6)
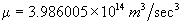
WGS 84 value of the earth`s universal gravitational parameter
(Eq.7)
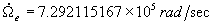
Computed mean motion rad/sec
(Eq.8)
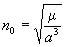
where a is semimajor axis.
Time from ephemeris reference epoch
(Eq.9)
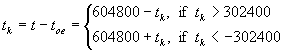
where t is GPS trasmit time, i.e. range/speed_of_light; and tk must account for week crossover.
Corrected mean motion
(Eq.10)
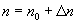
Mean anomaly
(Eq.11)
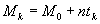
Kepler`s equation foe eccentric anomaly
(Eq.12)
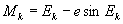
True anomaly
(Eq.13)
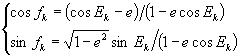
Eccentricity anomaly
(Eq.14)
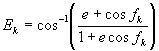
Argument of latitude
(Eq.15)
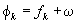
2nd harmonic pertubations
(Eq.16)
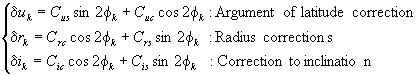
Corrected argument of latitude
(Eq.17)
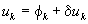
Corrected radius
(Eq.18)
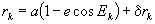
Corrected inclination
(Eq.19)
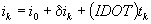
Position in orbital plane
(Eq.20)
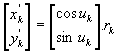
Corrected of longitude of ascending node
(Eq.21)
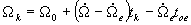
ECEF (Earth-Centered Earth-Fixed) coordinates
(Eq.22)
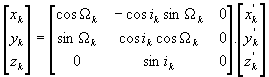
3. Basic Numerical Method
Linearizing Eq.5 gives
(Eq.23)

where
(Eq.24)
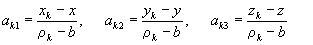
Eq.23 can be written in matrix form as
(Eq.25)
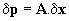
where
(Eq.26)
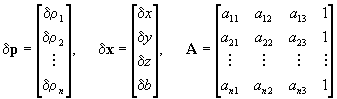
The solution of Eq.25 is
(Eq.27)
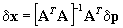
where [ATA]-1AT is the pseudo-inverse of A as non-square matrix has no true inverse A-1.
Based on Eq.27, we have the following algorithm to solve Eq.5
|

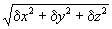 is less than an arbitrarily chosen threshold,
otherwise continue the following Step (7);
is less than an arbitrarily chosen threshold,
otherwise continue the following Step (7);